Huffman-Codes stellen ein vergleichsweise einfaches Mittel zur Datenkompression dar. Ähnlich wie beim Morse-Code liegt eine statistische Analyse der zu kodierenden Zeichen zu Grunde, die dazu dient, häufig vorkommenden Zeichen kürzere Codes zuzuweisen als solchen Zeichen, die seltener vorkommen. Das führt zu einem optimalen Code für genau die Daten, die analysiert wurden. Der Morse-Code hingegen beruht auf einer einmalig erfolgten Analyse (angeblich durch Auszählen der Lettern im Setzkasten der örtlichen Zeitung in Morristown, New Jersey) und ist für typische englische Texte optimiert.
Anders als beim Morse-Code wird beim Huffman-Code kein Trennzeichen zwischen den Symbolen benötigt. Es handelt sich um einen präfixfreien Code, das heißt kein Symbol ist Bestandteil eines längeren Symbols (wie z.B. "Bau" ein Präfix von "Baum" ist). Das ergibt sich aus der Art, auf die ein konkreter Huffman-Code erzeugt wird.
Eine fundamentale Einschränkung des Verfahrens ist, dass Sender und Empfänger über das gleiche Code-Wörterbuch verfügen müssen, d.h. dieses auf irgendeine Art und Weise mit übertragen werden muss (anders als es etwa bei LZW der Fall ist).
Die Erzeugung eines konkreten Huffman-Codes besteht aus folgenden Schritten:
In Huffman-Bäumen stellen die Blätter Zeichen aus dem Eingabealphabet dar, während innere Knoten lediglich der Verbindung dienen. Wie viele Kinder jeder innere Knoten haben darf hängt davon ab welche Art von Codes man erzeugen möchte -- für die Erzeugung von Binärcodes muss jeder innere Knoten genau zwei Kinder besitzen.
Die Codes der Blätter ergeben sich aus ihrer Position innerhalb des Baums und stellen gewissermaßen Wegbeschreibungen aus Sicht der Wurzel dar. Angenommen die linken Kinder werden durch 0 und die rechten Kind durch 1 adressiert, so bezeichnet der Code 1011 jenes Zeichen, das von der Wurzel aus durch den Pfad rechts-links-rechts-rechts erreicht wird.
Dadurch, dass für die Repräsentation von Zeichen nur Blätter zulässig sind, ergibt sich die Präfixfreiheit der Codes: solange die Folge unvollständig ist, endet die Wegbeschreibung auf einem inneren Knoten und keinem Blatt.
Damit der Code auch optimal ist, müssen die Zeichen (Blätter) so verteilt werden, dass seltener auftretende Zeichen tiefer hängen als solche Zeichen, die oft vorkommen. Dadurch sind die Wege (und damit die Codes) zu den selteneren Zeichen länger als für die häufiger auftretenden Zeichen. Der Algorithmus zur Erstellung solcher Bäme lautet:
Durch diesen Algorithmus werden die seltenen Zeichen zuerst verbaut und hängen im fertigen Baum stets tiefer als die häufigen Zeichen. Die Summenbildung berücksichtigt die Tatsache, dass große Teilbäume viele verschiedene, für sich genommen seltene, Zeichen beinhalten und somit die Wahrscheinlichkeit größer ist, dass irgendeins dieser Zeichen vorkommt. Wenn man ein paar Bäme von Hand aufzeichnet und damit experimentiert leuchtet das schnell ein.
Als Beispiel soll ein Huffman-Baum für den Satz "Das Pferd frisst keinen Gurkensalat" erstellt werden. Um das Beispiel kürzer zu halten soll auf die Unterscheidung von Groß- und Kleinbuchstaben verzichtet werden. Das Eingabealphabet hat also 15 Zeichen die sich wie folgt verteilen (in Reihenfolge des ersten Auftretens):
| Zeichen | d | a | s | _ | p | f | e | r | i | t | k | n | g | u | l |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Häufigkeit | 2 | 3 | 4 | 4 | 1 | 2 | 4 | 3 | 2 | 2 | 2 | 3 | 1 | 1 | 1 |
Die folgende Animation soll den Aufbau eines entsprechenden Huffman-Baums veranschaulichen.
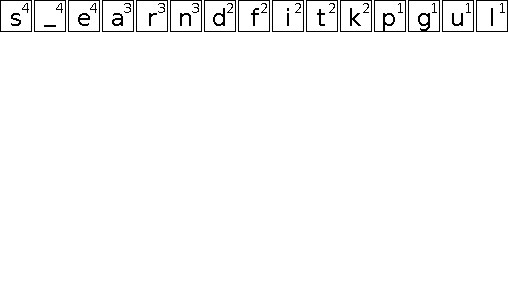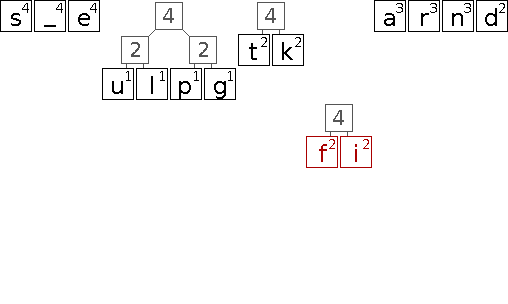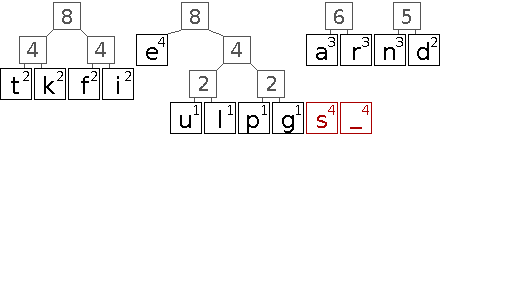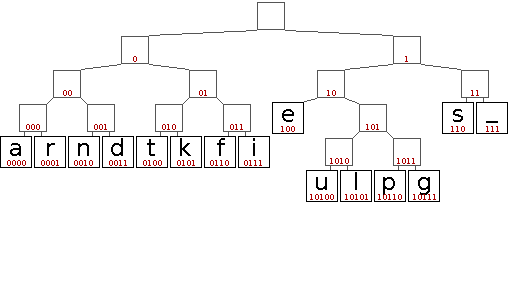
In diesem Beispiel gibt es eine Reihe von Entscheidungen die scheinbar willkürlich getroffen werden. Dazu zählt die initiale Anordnung der Zeichen gleicher Wertigkeit und darauf folgend das Einsortieren neu gebildeter Teilbäume. Da lediglich die Wertigkeit entscheidend ist, sind alle diese Entscheidungen äquivalent. Sie führen jedoch zu unterschiedlichen Bäumen und somit auch zu unterschiedlichen Codes. Das ist problematisch, wenn sowohl Sender als auch Empfänger einer kodierten Nachricht die Bäume bzw. Codes aus der Häufigkeitsverteilung der Zeichen ableiten, aber unterschiedliche Entscheidungen treffen. Daher muss entweder sichergestellt werden, dass der Algorithmus ähnlich implementiert ist, oder der fertige Baum bzw. das daraus resultierende Code-Wörterbuch mit übertragen wird.
Die Binärcodes aus obigem Beispiel lauten:
| Zeichen | d | a | s | _ | p | f | e | r | i | t | k | n | g | u | l |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Häufigkeit | 2 | 3 | 4 | 4 | 1 | 2 | 4 | 3 | 2 | 2 | 2 | 3 | 1 | 1 | 1 |
| Code | 0011 | 0000 | 110 | 111 | 10110 | 0110 | 100 | 0001 | 0111 | 0100 | 0101 | 0010 | 10111 | 10100 | 10101 |
Die Länge der Codes in Abhängigkeit zur Auftrittshäufigkeit ist gut erkennbar. Aber macht dieser Code die Nachricht tatsächlich kürzer?
Kodierter Text:
00110000 11011110 11001101 00000100 11111011 00001011 11101100 10011101 01100011 10010100 00101111 01111010
00001010 11000010 11000001 01010000 0100
Das sind 132 Bits (16,5 Bytes) für 35 Zeichen. Aber es wäre unfair für die normale Übertragung 1 Byte pro Zeichen anzusetzen, weil das Beispiel von Vornherein auf Kleinbuchstaben und Leerzeichen, also 27 Zeichen, eingeschränkt war. Mit einem "normalen" Binärcode wären hier 5 Bits pro Zeichen ausreichend. Aber auch damit wäre man bei 35 * 5 = 175 Bit (ca. 22 Bytes), d.h. der Huffman-Code hätte rund 25% eingespart.
Das Einsparpotenzial wächst mit den Unterschieden in der Häufigkeitsverteilung und findet sein Maximum, wenn ganz viele Zeichen überhaupt nicht auftreten, wohingegen normale Codes quasi jederzeit auf alle möglichen Zeichen vorbereitet sein müssen.
Ich habe ein Beispiel-Programm erstellt, das anhand einer Eingabedatei einen Huffman-Baum plus Code-Wörterbuch erstellt und berechnet, wie viel Platz die kodierten Daten benötigen würde. Die folgende Tabelle zeigt die Ergebnisse für eine Reihe gängiger Dateitypen.
| Art der Datei | Dateiformat | Größe vorher | Größe nachher | Verhältnis vorher/nachher |
|---|---|---|---|---|
| C++-Quellcode | ASCII | 5.008 | 3.247 | 64,8% |
| Text | ASCII | 35.147 | 20.252 | 57,6% |
| Text mit Tabellen und Diagrammen | 166.384 | 163.280 | 98,1% | |
| x86-Maschinencode (mit Debug-Symbolen) | EXE | 303.616 | 177.723 | 58,5% |
| x86-Maschinencode (ohne Debug-Symbole) | EXE | 42.496 | 30.592 | 72,0% |
| Archiv-Datei | 7-Zip | 23.253 | 23.253 | 100,0% |
| Archiv-Datei | PKZIP | 2.030.951 | 1.994.404 | 98,2% |
| Bild | Bitmap | 9.272 | 6.357 | 68,6% |
| Bild | JPEG | 2.717.480 | 2.689.816 | 99,0% |
| Audio | WAVE | 488.786 | 323.410 | 66,2% |
| Audio | MP3 | 5.361.536 | 5.350.390 | 99,8% |
| Video | MP4 | 31.174.008 | 31.174.008 | 100,0% |
Man sieht recht schön, dass sich bereits komprimierte Dateien (PDF, JPEG, MP3, ZIP-Archive) erheblich schlechter komprimieren lassen als Rohdaten (ASCII, Bitmap, WAVE). Das ergibt durchaus Sinn, denn andere Kompressionsverfahren beruhen ebenfalls darauf, Redundanz zu vermeiden und somit Dateien zu erzeugen, die den Wertebereich der 8-Bit-Bytes optimal ausnutzen.
| Datum | Version | Datei | Beschreibung |
|---|---|---|---|
| 2019-01-12 | 1.0 | huffman-1.0.zip | Demo-Programm (C++) |