Das Abtasttheorem ist erfüllt: fAbtast (12 kHz) ist mehr als doppelt so groß wie der höchstfrequente Anteil des Signals (5 kHz).
Hinweis: diese Seite wurde verworfen und wird nicht mehr gepflegt.
Bei jeder Abtastung eines Signals muß beachtet werden, daß die Abtastfrequenz ausreicht. Sie muß mindestens doppelt so groß wie der höchste Frequenzanteil des abzutastenden Signals sein, damit es fehlerfrei wiederhergestellt werden kann. Diese Gesetzmäßigkeit entdeckten Harry Nyquist und Claude Shannon in den 20er Jahren des 20. Jahrhunderts. Wird eine geringere Abtastfrequenz verwendet, entstehen Fehler die sich erst bei der Rekonstruktion des Signalverlaufs zeigen. Dabei entstehen sogenannte Alias-Frequenzen. Sie können nicht mehr vom echten Signal unterschieden werden, womit eine Filterung unmöglich ist. Der Fehler muß also bereits bei der Abtastung vermieden werden.
Man unterscheidet die Einfachverletzung (0,5 * fAbtast < fmax < fAbtast), Überverletzung (fAbtast < fmax < 1,5 * fAbtast) sowie Mehrfachverletzung (1,5 * fAbtast < fmax). Zur Veranschaulichung der Konsequenzen einer solchen Verletzung habe ich ein kleines Programm geschrieben. Es erlaubt die Generierung eines Signals, das entweder nur aus einer sinusförmigen Grundfrequenz besteht, oder aus einem Gemisch mehrerer Frequenzen. Ebenfalls einstellbar ist die Frequenz, mit der dieses Signal abgetastet werden soll. Die Ausgabe enthält die Rekonstruktionen nullter, erster und zweiter Ordnung.
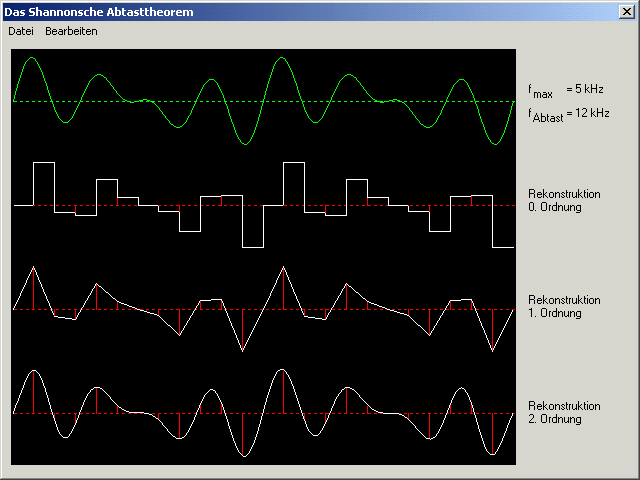
Hier ein Beispiel mit einem komplexen Signal bis 5 kHz und einer Abtastfrequenz von 12 kHz:

Das Abtasttheorem ist erfüllt: fAbtast (12 kHz) ist mehr
als doppelt so groß wie der höchstfrequente Anteil des Signals
(5 kHz).
Bei der Rekonstruktion nullter Ordnung wird der Wert beibehalten, bis der nächste Wert vorliegt. Dies ist die einfachste Form, und wird z.B. in CD-Playern genutzt. Bei ausreichend großer Abtastfrequenz ist die Ungenauigkeit, die sich durch die "Treppchen" ergibt, nicht hörbar. Bei niedriger Abtastfrequenz ergeben sich störende Effekte durch die hohen Frequenzen der rechteckigen Verläufe.
Die Rekonstruktion erster Ordnung entsteht, wenn die Abtastwerte durch lineare Interpolation verbunden werden. Das Ergebnis hat mehr Ähnlichkeit mit dem ursprünglichen Signal. Allerdings kann mit der Interpolation naturbedingt erst begonnen werden, wenn der nächste Wert bekannt ist. Sie ist also immer geringfügig zeitverzögert, und setzt eine Berechnung voraus.
Das Ergebnis der Rekonstruktion zweiter Ordnung sieht dem Original zum Verwechseln ähnlich. Hier wird jeder Punkt im Signalverlauf durch eine Funktion errechnet, die alle anderen Abtastwerte als Eingabe kennt. Sie ist relativ aufwendig und setzt eben die Kenntnis aller Abtastwerte voraus (wobei ab einer gewissen zeitlichen "Ferne" der Einfluß vernachlässigbar wird). Die genaue Funktionsweise ist mir nicht mehr bekannt, ich hatte das Programm direkt nach einer Vorlsung über Signalverarbeitung runtergehackt, und offenbar nicht viel davon verstanden. ;-)
| Datum | Datei | Beschreibung |
|---|---|---|
| 2004-10-21 | shannon.zip | Quellcode und Win32-Binary |